研究前沿
基于数据驱动的文物环境风险状态评估方法研究
原作者: 王琨,梁茹,侍洪波,谭帅,蔡兰坤,吴来明,徐方圆 |
来自: 文物保护与考古科学 |
发布时间:2024-11-6 10:52 |
查看: 919 | 发布者: coolcool |
摘要: 基于数据驱动的文物环境风险状态评估方法研究王琨1,梁茹1,侍洪波1,谭帅1,蔡兰坤2,吴来明3,4,徐方圆3,41. 能源化工过程智能制造教育部重点实验室(华东理工大学),上海 200237;2. 国家环境保护化工过程环境风险评价与控制重点实验室(华东理工大学),上海 200237;3. 馆藏文物保存环境国家文物局重点科研基地(上海博物馆),上海 200231;4. 上海 ...
王琨1,梁茹1,侍洪波1,谭帅1,蔡兰坤2,吴来明3,4,徐方圆3,41. 能源化工过程智能制造教育部重点实验室(华东理工大学),上海 200237;2. 国家环境保护化工过程环境风险评价与控制重点实验室(华东理工大学),上海 200237;3. 馆藏文物保存环境国家文物局重点科研基地(上海博物馆),上海 200231;在博物馆文物保护中,对环境风险监测和风险变量的及时定位有重要意义。然而,由于各个文物展馆的差异性,很难将某一展馆的环境风险划分标准应用于其他展馆,甚至无法应用到同一展馆的不同类型文物。除此之外,当风险出现时,博物馆无法及时锁定影响因素,延长了风险排除所需的时间。因此,结合上海博物馆江南文化艺术临展的连续监测数据,提出了一种针对纸质文物的环境风险状态评估二级监测框架,并按需求划分为“优、良、中、差”四个等级进行风险监测。首先,使用“优”数据集建立主成分分析(principal component analysis,PCA)模型并构建控制限用以挑选“优”数据,“差”数据集通过已有的PCA模型得到判断“差”等级的控制限;然后,使用“非优非差”数据集建立ReliefF-PCA模型并得到“良”“中”等级划分的控制限;最后,对应PCA模型和ReliefF-PCA模型分别使用贡献图和基于ReliefF算法计算权值的加权贡献图,以此量化风险,初步定位对环境指标存在影响的风险变量。通过两个评价模型构建的监测框架,为文物保存环境质量的评估和后续馆藏环境调控提供了一种更为科学的方案,有助于提高整个文物保护系统的效率。文物作为承载多种价值的重要载体,一旦受到损害便不可复原[1-2],随着文物保护意识的增强,文物健康受到越来越多的关注。博物馆作为保存和展览文物的场所,其环境指标是决定文物状态的重要因素[3],因此通过对环境指标进行监测并划分风险评估等级,有利于保证文物保存的优良环境,减缓环境因素对文物的损害[4],延长文物寿命。因为各个博物馆在不同地域环境差异较大且同一博物馆的不同展柜所展示文物类型有所不同[5-6],为了实现对文物展柜环境的监测和调控,都要求操作人员具有专业和长期的工作经验,这增加了博物馆环境风险状态评估的难度和排除风险环境因素的时间。并且,评估常采用的模糊理论[7]、层次分析[8]等方法的核心均在于影响因素的权重设置上,具有很强的主观性,评判标准并不完全统一,直接影响监测系统的准确率。除此之外,监测得到的大量历史数据信息并未得到充分挖掘[9]。为了克服以上问题,需要构建一个更为科学稳定的监测框架。近年来,以数据驱动技术为代表的监测方法逐渐应用于各个领域,它能够充分利用数据信息来定量描述馆藏文物关键环境变量和风险等级之间的关系,典型的方法已在文物保护领域初见成效。其中,K-means算法作为一种基于划分的聚类算法[10],可以在历史数据没有等级划分标签的情况下,根据分类数目的设置需求,以欧式距离为衡量指标自动进行环境风险状态划分[11]。但是,因为该方法建模时的历史数据并未使用专家经验提供的等级标签,且还存在离群点和需要预先指定聚类中心的问题,所以对聚类结果的影响较大[12]。因此,基于带等级标签的历史数据进行环境风险状态划分具有更高的可信度。PCA算法作为多变量统计的常用方法之一[13-14],能够对数据进行降维和主要信息的保留,具有去除数据相关性和减少噪声影响的优点[15]。张小红在此基础上提出了基于PCA和支持向量机(support vector machine,SVM)的综合文物健康风险评价方法[16],通过使用PCA降低维度后建立SVM多分类模型来对风险进行评估。但是,SVM的结构决定其存在对大规模数据训练困难的问题。PCA不仅可以作为一种降维方法,还可以利用其构建的统计量求取环境风险划分的控制限。具体地,在数据按最大方差标准特征分解后,利用挑选出的主成分构建T2统计量[17],并使用核密度估计(kernel density estimation,KDE)算法求取“优”和“差”数据集对应的控制限,它可以实时监测出“优”和“差”等级的数据,否则为介于两个等级之间的中部数据。但是,随着等级划分要求更加精细,普通的三等级划分已经不能完全满足实际需求,此时,PCA算法对于“非优非差”中部数据的等级划分便存在难度。ReliefF是一种特征提取算法[18],陶阳等提出的ReliefF-PCA算法[19]最早应用在化工领域,从监测故障的角度出发,利用ReliefF算法计算权值,挑选出PCA中能够区分正常数据和故障数据的主元。利用这个思想,当训练数据为“非优非差”的中部数据时,用该方法所选主元构造的控制限能够提高中部数据多等级划分的准确性。当实时监测出的环境等级为“非优”状态时,为了保证文物的良好保存条件,需要量化风险,及时定位并调控风险变量。在PCA模型中,利用贡献图的方法能够实现这一功能[20];在ReliefF-PCA模型下,则将ReliefF算法计算得到的权值应用到贡献图中,使得加权贡献图能够更准确地定位风险变量。本工作针对上海博物馆江南文化艺术临展的连续监测数据,提出了一种环境风险状态评估的二级监测框架,利用PCA算法和ReliefF-PCA算法进行“优、良、中、差”四等级划分,并基于贡献图及时定位风险变量,有效地分配管理资源。上海博物馆作为一座大型中国艺术博物馆,在“春风千里——江南文化艺术展”临展期间为陈列的珍贵文物提供了良好的展厅、展柜环境,工程部将展厅的空调温度设定为20℃,相对湿度设定为55%。本工作以存放纸质文物的展柜4所采集的环境数据作为研究对象,仪器设定的测量间隔为10 min,在线监测的环境指标包括展厅、展柜内的温度、相对湿度及露点等。将采集的训练数据记为X={x1,x2,···,xn},X∈Rn×m,其中n为采集的样本数,m为环境变量数。因为具有不同量纲的环境变量会导致取值的分散程度差异较大,所以常采用z-score方法对数据进行预处理来消除此问题带来的影响,如式(1)所示。(1)
式中:mean(X)和std(X)分别表示训练数据X的均值和标准差。为了简化符号表述,之后的zi仍用xi表示。标准化后的X根据已有的等级标签分为“优”“良”“中”“差”,分别用XA、XB,1、XB,2、XC表示。对已经过预处理的数据XA,构建其协方差矩阵S,并对S进行特征值分解:(2)
式中:对角矩阵Λ∈Rm×m包含降序排列的非负实特征值λi(i=1,2,···,m),负载向量V∈Rm×m。为了更好地获取数据的变化量和保留数据的主要信息量,一般选择将前k(k<m)个特征值对应的负载向量进行保留,记为P∈Rm×k。然后,利用负载矩阵P构建PCA模型,样本数据XA可以按式(3)展开:(3)
式中:为模型估计的数据矩阵;T为得分矩阵;E为残差矩阵。随后,构建Hotelling T2统计量来描述主元空间的变化,如下式:(4)
根据KDE算法估计XA所对应统计量的控制限T2A[21]。ReliefF-PCA算法在PCA主元分解的基础上,进一步挑选对样本集分类效果更显著的特征向量,并以ReliefF算法计算的权值构成权重矩阵来代替PCA的对角矩阵Λ。对中部数据,将“良”数据集和“中”数据集扩展为训练数据,并按公式(1)的形式进行标准化。(5)
然后,随机选择X*中第r行作为样本xr,当r≤n1时,xr为正常样本;r>n1则为故障样本。利用欧式距离分别在数据集XB,1和XB,2中各选出s个与xr近邻的样本构成两个新的数据集,记为Xh和Xm,根据如下公式计算两数据集中每个样本的T2统计量:(6)
(7)
式中:Xhq和Xmq为两数据集中的第q(q=1,2,···,s)个样本;Pnp为负载矩阵的第p个负载向量;Tnp为得分矩阵对应的第p个得分向量。为了简化表示,分别将具有s个近邻样本对应的T21和T22记为D1和D2。计算D1和D2中每个样本与xr样本在各负载向量下的距离,记为Dh和Dm,计算公式如下:(8)
(9)
式中:i为第i(i=1,2,···,s)个样本;j为第j(j=1,2,···,m)个负载矩阵。R(j)为xr在第j个负载向量下的统计量值,具体表述如式(10)。(10)
对以上抽样操作和距离计算l次,按式(11)累计计算距离差值作为选择负载向量的依据,并将其作为对应负载向量的权值W,取代PCA中对角矩阵中的数值。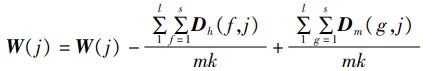 (11)
(11)
对不同负载向量对应的权值按降序排列,记为W*,选择出前c个负载向量和权值构建统计量T*2如下:(12)
式中:x2为标准化后的样本;Λ∈Rc×c为W*前c个权值构成的对角矩阵;P*∈Rm×c为对应的负载矩阵。文物保护规划提出至今,经历了不断完善的过程,随着文物向文化遗产认知逐渐拓展[22],博物馆也越来越关注文物所处环境对文物保存的影响。因而提出环境风险状态评估的二级监测框架来减缓文物的老化,并在环境等级未达标时,利用基于贡献图的方法对潜在的影响变量初步定位,以便操作人员及时调控。在多等级数据划分中,因为“优”和“差”两类数据有较明显的特征,在各类中易于被区分,而“非优非差”的中部数据之间界限较为模糊,在某些情况下仅依靠专家经验也有较大的区分难度,这为博物馆的文物保护工作增加了困难。因此,提出一种二级划分策略,具体描述如下:1)首先,使用“优”数据集XA建立PCA模型,根据式(4)求统计量并得到区分“优”与“非优”的控制限T2A;再将“差”数据集XC带入已建好的PCA模型中得到一系列统计量值,并将统计量中的最小值作为区分“差”和“非差”的控制限T2C。对测试数据“优”和“差”的判断逻辑如下: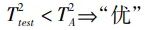 (13)
(13)
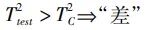 (14)
(14)
当测试数据的统计量介于T2A和T2C之间,则无法判断该数据属于中部数据的哪个具体等级,此时需要进入下一级判断。2)对于“非优非差”中部数据集XB={XB,1,XB,2}这里用XB,1,XB,2表示“良”、“中”等级数据,具体的命名对照现场实际需求进行改动。采用ReliefF-PCA算法并对照2.2中的步骤计算得到统计量和能够区分两类数据的控制限T2B。对测试数据的判断逻辑如下: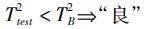 (15)
(15)
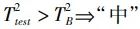 (16)
(16)
需要注意的是,文中是针对上海博物馆的实际需求才设计为四个等级,并以此为例来进行详细说明。该框架不仅局限于四个等级的划分,当等级超过四个时,对“非优非差”的中部数据可通过ReliefF-PCA算法多次计算,划分为更多等级。在实际应用中,环境风险等级“非优”是由各变量的超限程度决定的,当出现该状态时,亟需找到导致风险的关键变量,从而使严重的风险先得到有效控制和管理。但是,博物馆中排查变量用时普遍较长,因而,在实时监控中若出现“非优”情况,采用贡献图的方法对风险变量进行初步定位,能够有效缩短排查和调控时间。对照环境风险的二级划分策略,贡献图的构造也有部分差别,具体构造步骤为:1)当环境风险判断为“差”时,利用对应PCA算法的贡献法来确定超限环境变量。第i个超限测试样本xi中第j个变量的贡献值计算如下:(17)
2)当环境风险判断为其他的中部等级时,对应ReliefF-PCA算法,使用W*加权的贡献图方法能够更加准确地定位超限环境变量,使该变量的贡献值更加突出。因而,在第二层级中的贡献值计算如下:(18)
式中:P*W(j)表示P*经过加权的第j个负载向量。(19)
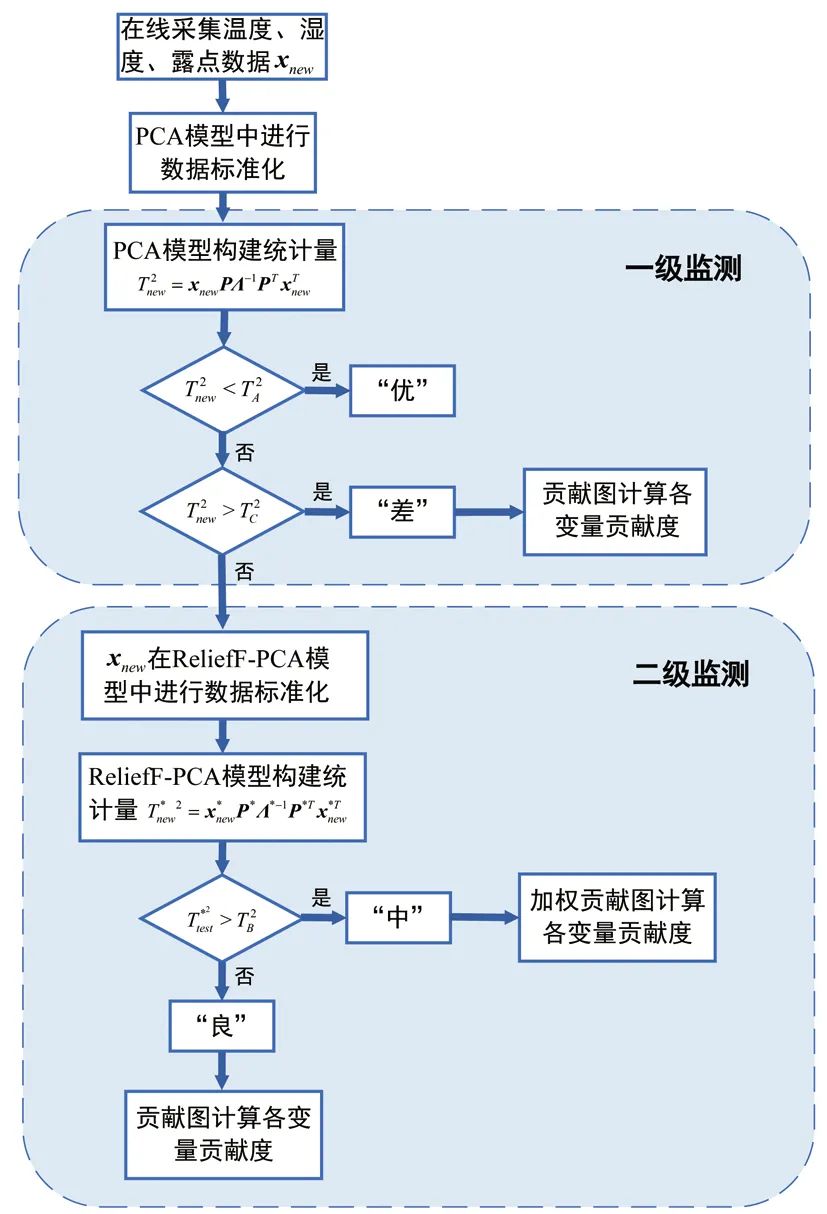
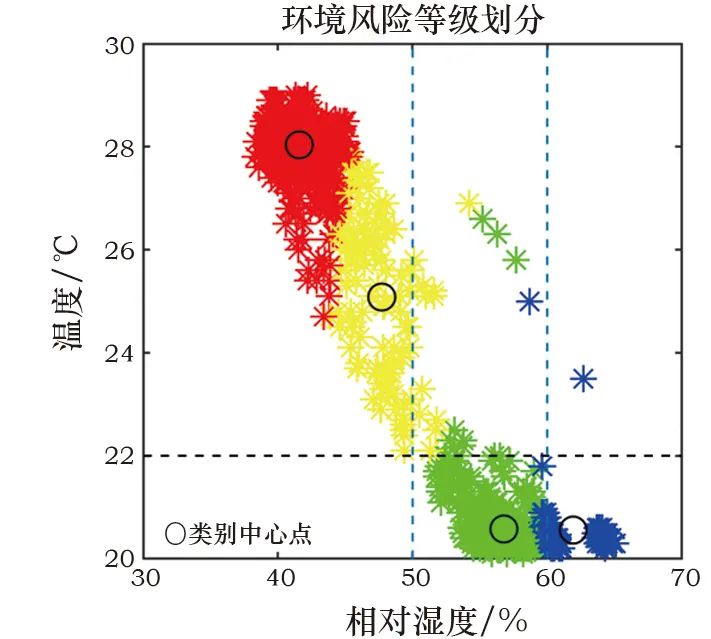
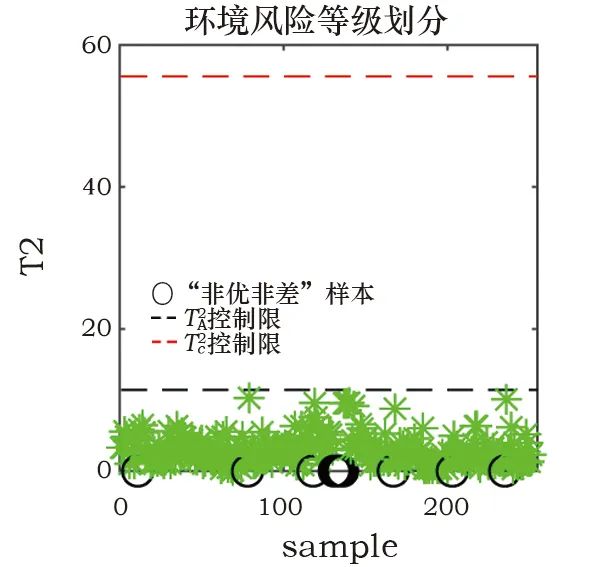
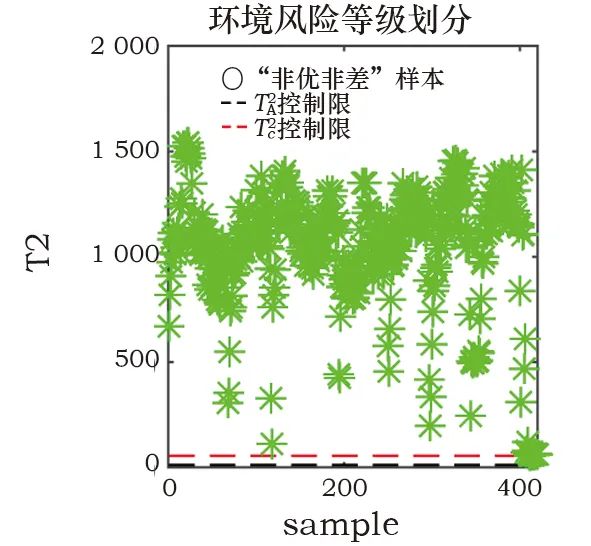
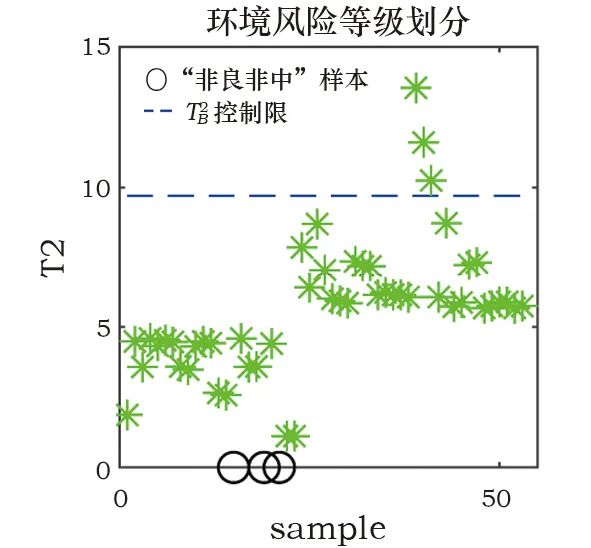
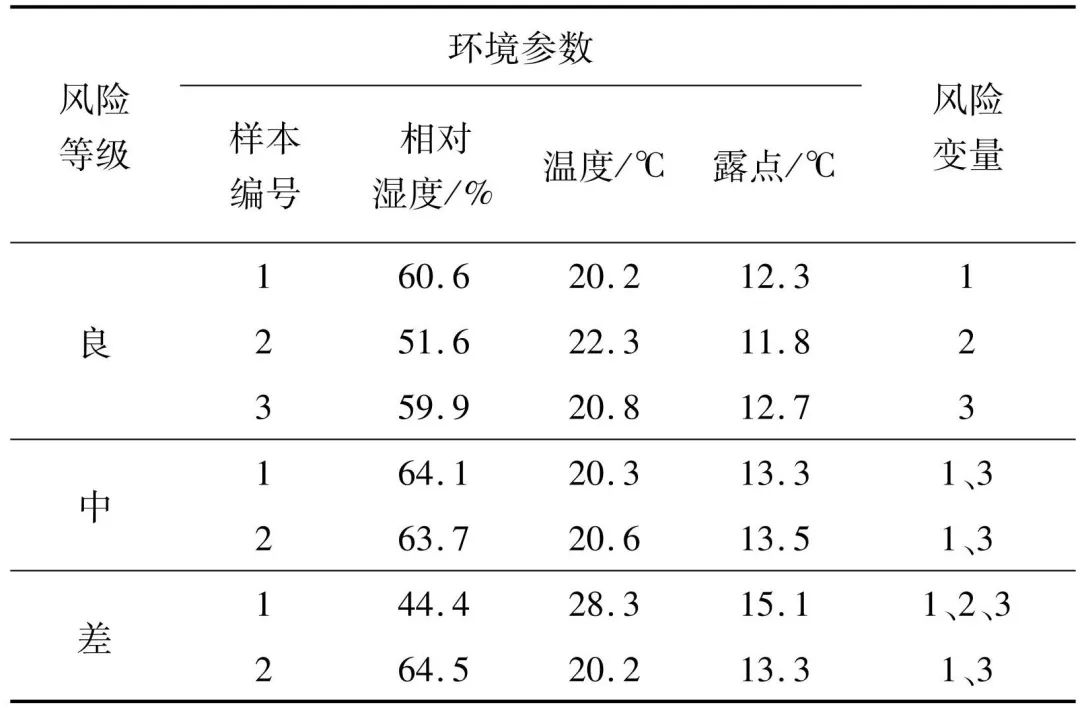
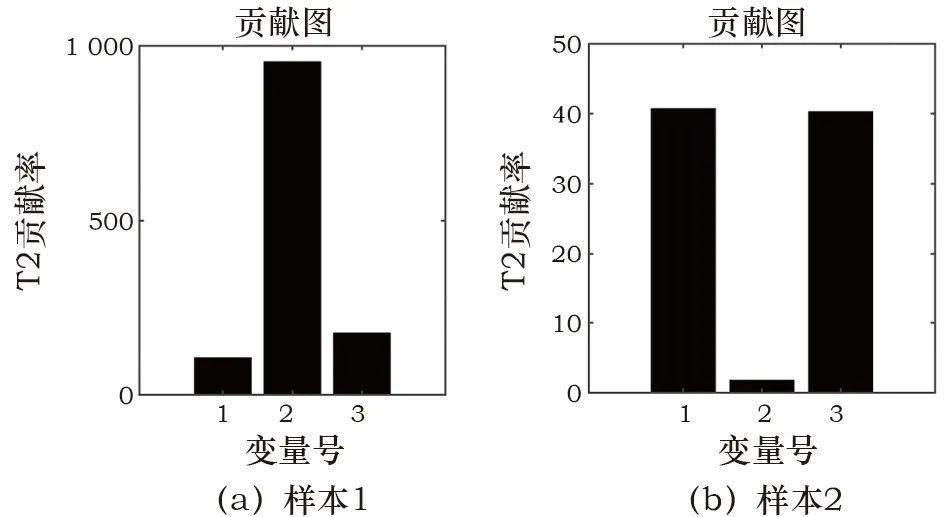
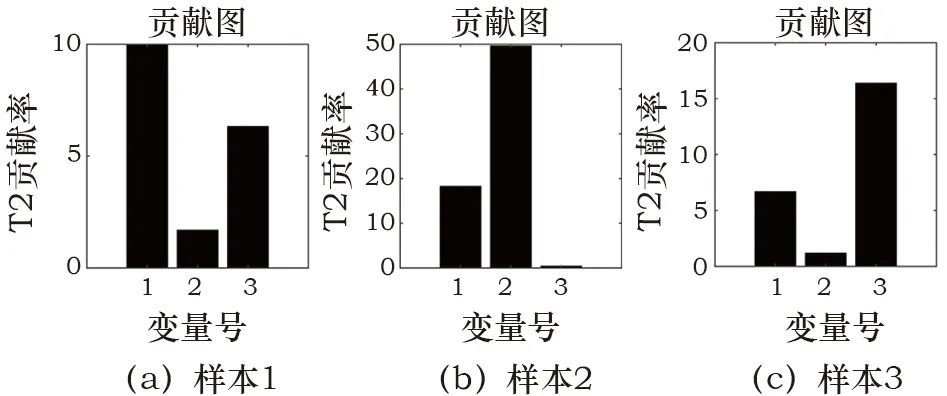
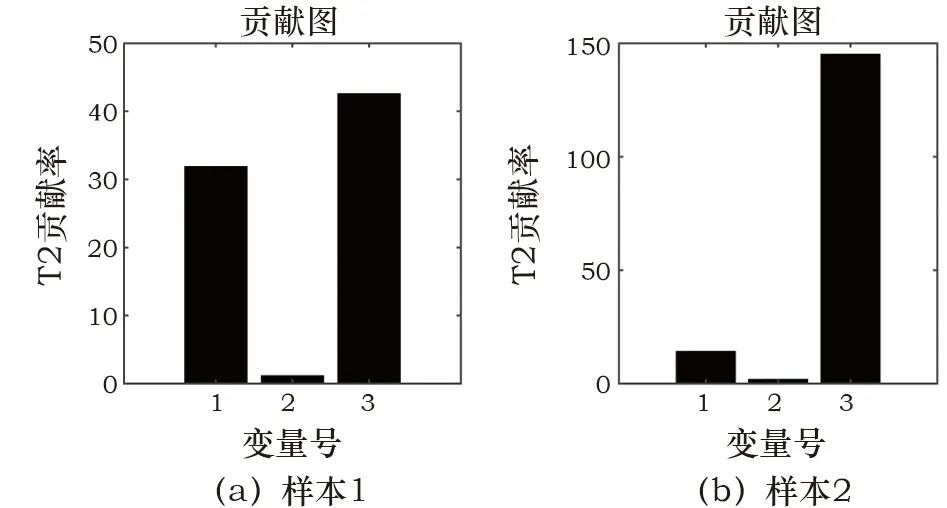
式中:W*(j)为经过降序排列后的第j个权值,是克罗内克积。为了实现对在线实时数据的监测,将环境风险划分为多个等级,利用已经得到的控制限T2A、T2B、T2C和二级划分策略进行判断,最后基于贡献图方法来区分不同变量的贡献度,初步定位相关变量。针对上海博物馆江南文化艺术临展的在线监测流程如图1所示。Fig. 1 Online monitoring process for environmental risks本工作使用上海博物馆江南文化艺术临展展柜4的纸质数据进行实验,并和目前常用的K-means算法进行对比,来说明监测方案的有效性。根据实际需求将四个等级命名为“优、良、中、差”。展柜4用于建模的历史数据为2 657个,具有温度、相对湿度及露点3个变量,根据历史评估可知,其中“优”为1 127个,“良”128个,“中”为89个,“差”为1 313个。用于测试的“优”“良”“中”“差”数据个数分别为251、53、20、420。在实验参数设置中,将所有统计量的置信度设为α=99%,为保证PCA和ReliefF-PCA的方差贡献率均为90%,则对应的主元个数k=3和c=2,取样次数l=50。K-means算法中的类别数量设置为4。使用PCA算法和ReliefF-PCA算法组成的二级监测框架对四类测试数据的环境风险状态进行划分,并用K-means算法作为对比,结果见表1。表中显示,对“优”等级的划分二者相差不大,均有较高准确率,K-means算法对“中”等级的划分和二级监测框架对“差”等级的划分准确率均达到100%。值得注意的是,K-means算法对“良”等级的划分很差,这表明该算法对不同等级的划分效果相差很大,这种不平衡性也体现在平均准确率被拉低,使之远小于二级框架的划分效果。Table 1 Accuracy of environmental risk status assessment (%)为了进一步分析K-means算法造成这一局限性的原因,使用训练数据在湿度和温度指标下的二维聚类图来说明。使用二维图作为展示是为了便于观察数据之间的分散关系,选择相对湿度和温度两个指标是因为ASHRAE2007美国采暖、制冷与空调工程师协会[23]对二者有明确的“优”划分标准,调控的目标值分别为55%和20℃。图2中可以看出,四种颜色的点代表了四种不同等级的数据,由“优”标准划分的区域可以判断绿色点为“优”等级的样本,但是“优”区域所包含的点并非只有绿色一类,绿色的样本点也并非全部被包含在该区域里。以上表明K-means算法在没有等级标签的指导下仅使用欧式距离进行划分的方式并不合理,在训练模型阶段就没有将四类样本进行准确划分,因而在线测试时会出现各类划分效果相差甚大的现象。图 2 K-means算法对训练数据的四等级风险划分Fig. 2 Four-level risk division of the training data by the K-means algorithm为了更直观地说明二级监测框架的结果,如图3~6所示。在第一级监测中对“优”和“差”测试数据进行判别,可以将“差”类型的样本全部划分出来,这在实际应用中能够及时对恶劣的保存环境做出报警;而对于“优”样本的划分几乎均在控制限以下,只有少数几个点被误报为“良”。第二级监测中,“良”的划分结果有3个超限被判别为“中”,也有3个在第一级判别中便被误划分为“优”的样本;对于“中”测试数据的划分,则有5个被误判为“差”。“良”“中”等级的划分效果有所下降,是因为用于训练的历史数据中,“优”“差”的判别条件更加统一而准确,而“良”“中”在专家没有统一标准进行评判时,难免会在两种类别中掺杂误判样本,并且该两类样本数量偏少,导致二者对应的数据多样性变少,当出现与训练样本相差较大的同等级样本时,更易导致误分类。综上对比两种算法,二级监测框架的风险状态划分更符合实际需求。数据的三个变量相对湿度、温度、露点分别对应标号1、2、3。当等级划分为“非优”时,需要衡量影响环境状况的不同影响因子,及时调控以减少对文物的折损。表2为“良”“中”“差”三个等级分别对应的几个典型样本,并列出各样本的环境风险变量。“良”的三个样本分别对应三个变量略有不达标的情况,而“中”“差”的产生因为常由多变量超标或单变量大幅度超标导致,所以各取两个样本以作表示。Fig. 3 “Excellent” data discrimination resultsFig. 4 “Poor” data discrimination resultsFig. 5 “Good” data discrimination resultsFig. 6 “Medium” data discrimination resultsTable 2 Four types of testing data对应第一级PCA方法的贡献图定位“差”等级的风险变量如图7a~7b所示,对照表中的风险变量可以看出,图7a贡献度最突出的是变量2,变量1和3相差不大,而实际中三者均超标,说明在这种情况下,贡献图无法确定风险变量是只有一个还是三个,因为当三个变量均不符合预期时,贡献图往往体现的是哪个变量对超限的影响更大,此时这个变量便是最需要调控的;图7b中贡献度突出的值为变量1、3,与实际的超标情况相吻合。“良”等级的贡献图如图8a~8c所示,在三种情况下它们均可准确定位超标变量。Fig. 7 Contribution plot of the “poor” sampleFig. 8 Contribution plot of the “good” sample在第二级监测中,由对应ReliefF-PCA算法的加权贡献图来计算每个变量的贡献度值,“中”的贡献图如图9所示。其中,图9a风险变量对应的贡献度都很显著,而图9b中变量1虽然也排居第二,但和3的贡献度相差较大,这是由不同变量的超限程度不等同导致的。Fig. 9 Contribution plot of the “medium” sample以上海博物馆江南文化展厅为研究实例,提出了一种基于PCA算法和ReliefF-PCA算法的环境风险状态评估二级监测框架。利用该方法对实时数据进行“优、良、中、差”四个等级的风险划分。首先,在第一级对“优”“差”等级的数据进行筛选,剩余的数据在二级监测中被再度划分。最后,“非优”等级的数据基于贡献图初步定位影响环境等级的变量,且能定量地体现各变量的超标程度。经过与K-means算法的对比实验,可以有效划分纸质文物环境风险等级,且能够通过风险变量定位为操作人员的在线调控提供初步参考,有针对性地改善文物保存环境,尽可能减轻文物损坏。
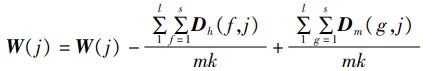 (11)
(11)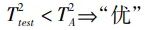 (13)
(13)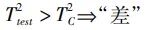 (14)
(14)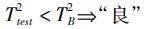 (15)
(15)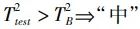 (16)
(16)